Золотое сечение: Самый раздутый миф в дизайне
Золотое сечение — это полный нонсенс в дизайне. И вот почему.
В мире искусства, архитектуры и дизайна золотое сечение завоевало потрясающую репутацию. Великие гении, включая Корбюзье и Сальвадора Дали, использовали эту пропорцию в своих работах. Парфенон, Пирамиды в Гизе, полотна Микелянджело, Мона Лиза и даже логотип Apple якобы построены на его основе. Это бред. Эстетика золотого сечения — это просто современная байка, миф. Многие дизайнеры им пренебрегают, а если и используют, то не стесняются преуменьшать его значение. Кроме того, у этой пропорции нет никакой научной подоплеки. Те, кто верят, что за красотой золотого сечения кроется математика, попались на крючок 150-летней давности. Пользователь FlickrSébastien Bertrand
Что такое золотое сечение?
Изначально описанный в Элементах Эвклида 2300 лет назад, этот термин гласит: два объекта находятся в золотой пропорции, если соотношение между ними идентично отношению их суммы к большему из двух элементов.
Золотое сечение всегда немного неточное.
Простым языком: если у вас есть два объекта (или один объект, который можно разделить на два, по аналогии с золотым прямоугольником), и если после вышеописанной математики, вы получите число 1.6180, обычно считается, что два объекта демонстрируют золотое сечение. Но есть одна проблема. Когда вы все-таки посчитаете, то сама пропорция не равна 1.6180. Она равна 1.6180339887… И десятичная часть уходит в бесконечность. “Собственно говоря, невозможно подобрать примеры золотого сечения в реальном мире, потому что это иррациональное число”, — заявляет Кит Девлин, профессор математики Стэнфордского университета.
Золотое сечение — это как эффект Моцарта
Конечно, это педантизм. Неужели 1.6180 — недостаточно точно? Возможно, и достаточно, если бы было какое-то научное обоснование того, что именно золотое сечение позволяет нам считать объекты вроде Парфенона или Моны Лизы эстетически приятными. Но это не так. Девлин считает, что сама идея, будто золотое сечение имеет какое-то отношение к эстетике, исходит от двух людей, один из которых был неправильно истолкован, а второй это толкование и обнародовал. Первый человек — Лука Пачоли, францисканский монах, который написал книгу под названием De Divina Proportione в далком 1509 году, и она была названа в честь золотого сечения.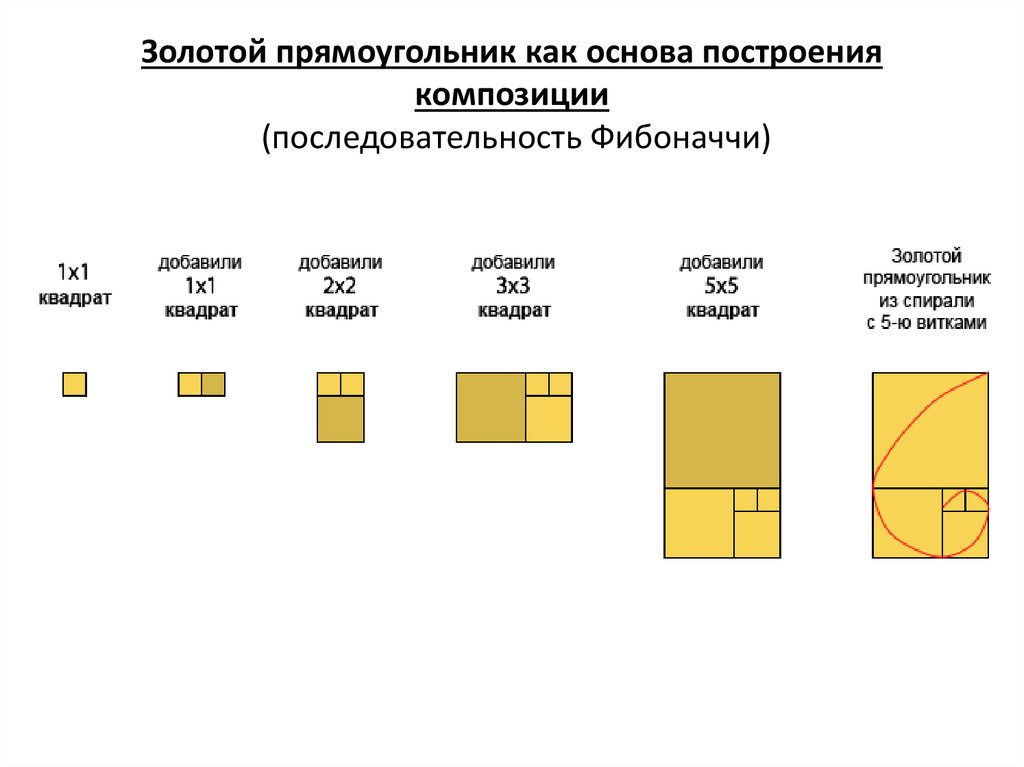
Он был очень многословным. Единственной проблемой Цейзинга было то, что он видел закономерности там, где их не было. Например, Цейзинг доказывал, что золотое сечение можно применить к человеческому телу, взяв рост человека от пупка до пальцев ног, поделив его на полный рост. По словам Девлина, это всего лишь произвольные части тела, слепленные в формулу. Он говорит: “При замерах чего-то столь сложного, как человеческое тело, очень легко найти примеры разных пропорций, близких к 1.6”.В моей собственной работе я даже не найду примера использования золотого сечения.
Но это не имеет никакого значения. Теории Цейзинга стали невероятно популярны, и Девлин называет их “эквивалентом эффекта Моцарта 19-го века”. Эффект Моцарта гласит, что прослушивание классической музыки повышает интеллект. В 20 веке известный швейцарско-французский архитектор Ле Корбузье положил золотое сечение в основу своей системы антропометрических пропорций “Модулора”. Дали нарисовал свой шедевр “Тайная вечеря” на холсте в форме золотого прямоугольника.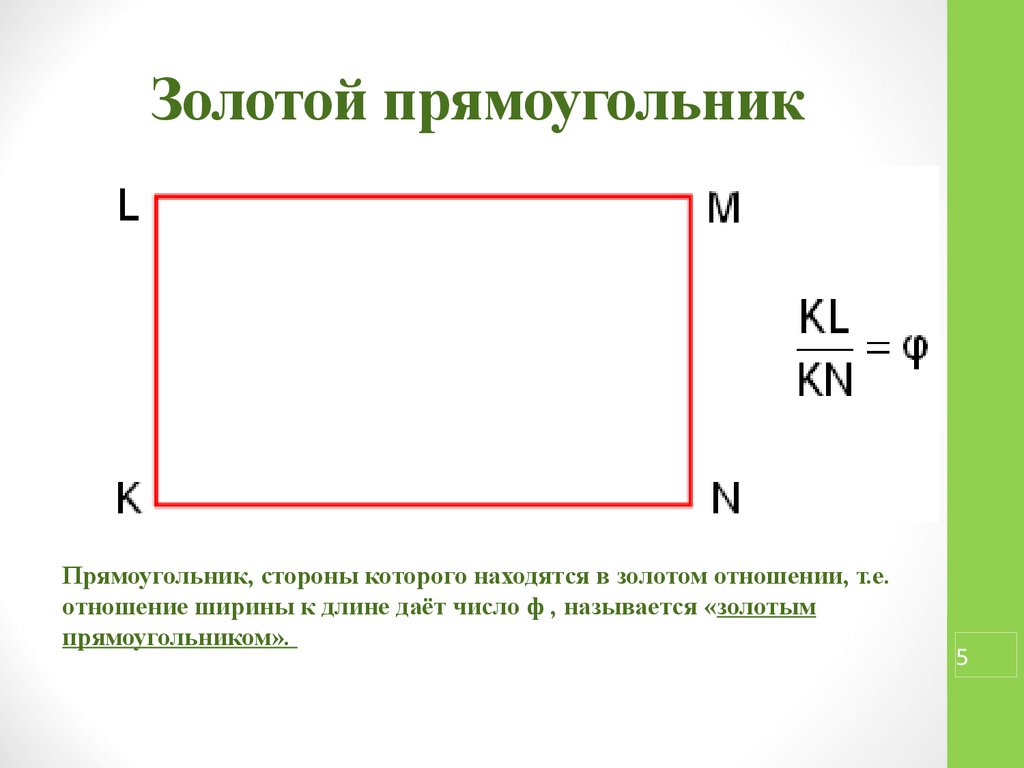
Тем временем историки искусства начали просматривать и другие шедевры, пытаясь отыскать золотое сечение в Стоунхендже, полотнах Рембранта, Шартрском соборе и работах Сёра. Связь между золотым сечением и красотой превратилась в самую раздутую утку в мире искусства, архитектуры и дизайна. Ian Yen на Yanko Design
На самом деле, вы не очень-то и предпочитаете золотое сечение
В реальном мире людям не особо необходимо золотое сечение. Девлин совместно с кафедрой психологии Стенфордского университета в течение многих лет опрашивал сотни студентов, какой прямоугольник их любимый. Он показывал разные прямоугольники студентам, а затем просил их выбрать наиболее понравившийся. Если бы оды золотому сечению были оправданы, студенты бы выбирали прямоугольники, близкие к золотому. Но это было не так. Они выбирают их произвольно. И если вы попросите их повторить свой выбор, они выберут другие прямоугольники. “Это очень полезный пример для демонстрации сложности человеческого восприятия”.
Многие современные дизайнеры не считают его полезным
Дизайнеры, с которыми мы обсуждали золотое сечение, не видят в нем особой пользы. Ричард Мейер, легендарный архитектор, автор Центра Гетти и Музея современного искусства в Барселоне, отмечает, что в начале своей карьеры у него был архитекторский треугольник, который соответствовал золотому сечению, но он никогда не создавал свои здания по золотому сечению. “В мире такое множество других чисел и формул, которые важнее при проектировании зданий”, — говорит Мейер, ссылаясь на формулы по расчету максимальных допустимых размеров пространств зданий, или на формулы расчета структурной нагрузки.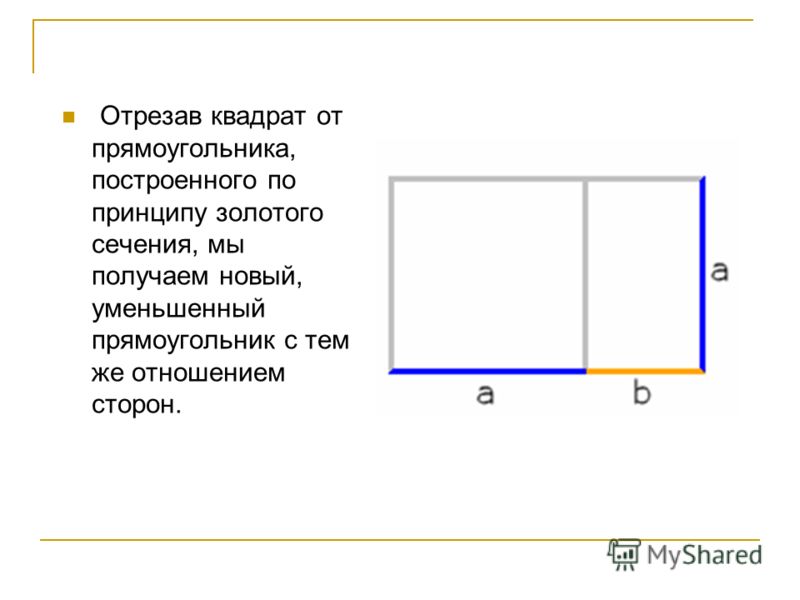
Почему этот миф так популярен?
Если ценность золотого сечения так незначительна, почему же этот миф процветает? Девлин поясняет это просто: “Мы создания, генетически запрограммированные видеть паттерны и искать смысл. В нашей ДНК не зашифрована способность мириться с условными вещами вроде эстетики, поэтому мы пытаемся доказать их с помощью нашего часто ограниченного математического видения.
Большая часть людей не понимает математику, и даже не может понять, как формула вроде золотого сечения применяется к сложной системе, так что и проверить себя они не могут. Люди думают, что повсюду видят золотое сечение, в природе и в любимых объектах, но они не могут это обосновать. Они — жертвы своего природного желания найти смысл в разных объектах вселенной, но из-за недостаточной математической грамотности они не могут понять, что обнаруживаемые закономерности иллюзорны”. http://ux.pub/zolotoe-sechenie-v-dizajne-interfejsov/
Перевод статьи JOHN BROWNLEE
Основные построения золотого сечения — Записки недизайнера — LiveJournal
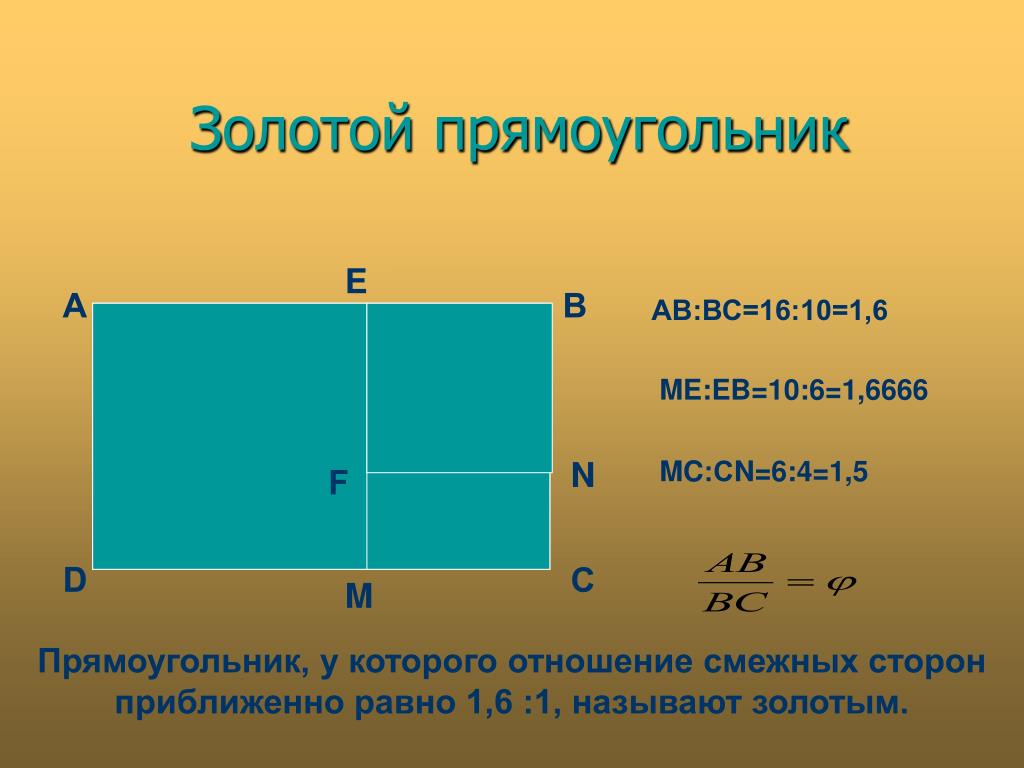
На практике при выборе формата листа (картины) часто используют «классические» пропорции сторон прямоугольника, в котором отношение меньшей стороны к большей составляет число 0,6180339, а большей к меньшей — 1,6180339. Эти числа с древнейших времён называют золотыми, а отношение величин, необходимое для их получения, известно как золотая пропорция или золотое сечение.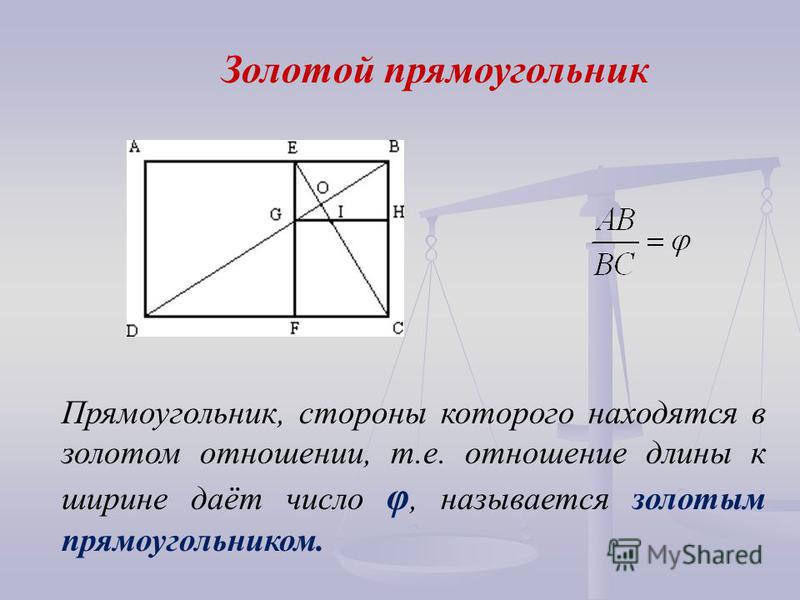
Основа учения о гармонии мира, выраженная в числовых отношениях, была заложена древнегреческим учёным-математиком Пифагором (VI в до н.э). Им представлено золотое сечение как одна из закономерностей, математически точно определяющая наиболее красивое и гармоничное соотношение частей целого, разделённого на две неравные половины.
На соотношении частей отрезка в пропорциях золотого сечения основано построение прямоугольника. С помощью диагоналей осуществляется членение его на составные части, при котором образуется динамика пропорциональных фигур — квадрата, прямоугольника, а также прямоугольного и равнобедренного треугольников.
Т.о., используя диагонали можно получить последовательный ряд увеличивающихся прямоугольников, с соотношением сторон — 1:√ 2, 1:√3, 1:√4, 1:√5, производных от квадрата.
При стороне √4 образуется прямоугольник с удвоенным квадратом. При стороне √3 образуется два прямоугольных треугольника, у которых общая гипотенуза является диагональю прямоугольника, равная удвоенной величине меньшего катета (т. е. стороне квадрата), и они имеют острые углы 30 и 60 градусов.
Диагональ используется и в построении последовательно увеличивающихся квадратов, создающих «динамическое» развитие их величины.
В этом построении сторона каждого последующего квадрата относится к стороне предыдущего, как диагональ квадрата к его же стороне. Эти преобразования иногда называют «активным квадратом».
Геометрическая система динамических пропорций квадрата, прямоугольника и треугольника были основой в создании архитектурных сооружений в ранний период Древнего Египта. Кроме того, в условиях примитивной техники архитектурного строительства в те далёкие времена постоянно требовалось восстановление перпендикуляра к прямой, которое осуществлялось тогда при помощи верёвки с 12 узлами. С использованием такого приспособления получался прямоугольный треугольник с отношением строно — 3:4:5, который впоследствии стали называть египетским. В настоящее время на его основе строят прямые углы и проводят перпендикуляры к концу отрезка.
С древнейших времён золотое сечение используется в практике построения различных изображений. Это способствует созданию гармоничных образов и уравновешенности пропорций во всём, что на окружает. Пропорции золотого сечения присутствуют в мамематике, и особенно в геометрии, в изобразительном искусстве, в быту и в природе, в растительном и животном мире.
Золотое сечение получило широкое развитие в математике. Так, в XVI веке итальянский учёный Фибоначчи выстроил математический ряд цифр, при котором последующее число определяет сумму двух предыдущих — 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. Кроме того, устанавливается и другая зависимость этих чисел, при которой отношение каждого последующего к предыдущему выражается числом 1,618…, а предыдущего к последующему — 0,618. Таким образом, в этом математическом ряду образуется взаимосвязь чисел, содержащая пропорции золотого сечения.
Особенно часто золотое сечение используется в геометрии при делении окружности на равные части и построении правильных многоугольников.
В звёздчатом многоугольнике — пятиконечной звезде, каждая точка пересечения её сторон делит их на две неравные части в пропорциях золотого сечения.
С древнейших времён золотое сечение применялось в различных видах изобразительного искусства — в архитектуре, вкульптуре, живописи. Парфенон — классический пример применения золотого сечения в архитектуре.
Особенно широко использовал в своём творчестве соотношение величин золотого сечения Леонардо да Винчи, которое он назвал «божественная пропорция».
Числовой гармонии золотого сечения подчиняются также античные статуи греческого искусства, отражающие пропорции идеально сложённого человеческого тела.
Золотое сечение применяют в начертании букв и цифр различного шрифта.
Золотое сечение часто используют в определении величины прямоугольника при заданной его большей или меньшей стороне. Если у прямоугольной картины задана длина (АВ), то её высоту (АС) определяют следующим построением:
Сначала из конца отрезка (В) проводят дугу, равную его половине до пересечения с перпендикуляром (АО=ОВ=ВД). Полученную точку Д соединяют прямой с другим концом отрезка (А). Затем из точки Д проводят дугу радиусом ВД до пересечения с этой прямой и отмечают точку Е. Дуга, проведённая из конца отрезка А радиусом АЕ определяет по вертикальной прямой точку С и искомую высоту картины АС.
Если задана высота картины (АС), то её длину (АВ) определяют другим построением. Сначала строят квадрат АСДЕ со стороной равной АС. Затем из середины стороны квадрата (О) проводят дугу радиусом ОД и получают на горизонтальной прямой точку В, которая определит искомую длину стороны прямоугольной картины АВ.
По прямоугольнику с золотыми пропорциями можно построить любой величинны подобный формат листа.
Для этого его накладывают на лист бумаги в один из его углов (А) и проводят в нём диагональ. Затем от точки А откладывают заданный размер горизонтальной или вертикальной стороны формата листа и через его конец проводят перпендикуляр до пересечения с диагональю, которая определит вторую сторону прямоугольника.
Источник: М.Н. Макарова «Практическая перспектива»
Tags: Золотое сечение
Золотое сечение породило новую красивую кривую: спираль Харриса | Алекс Беллос
Математики любят придумывать что-то новое. Теорема, может быть, лемма или даже просто следствие.
Эдмунд Харрис открыл кривую.
Харрисс преподает математику в Университете Арканзаса. Он также художник, и его интеллектуальные поиски начались с формы, которая, как известно, принадлежит как науке, так и искусству: золотой прямоугольник:
Золотой прямоугольник делится на квадрат и меньший золотой прямоугольник.Золотой прямоугольник — это прямоугольник, стороны которого пропорциональны золотому сечению, равному 1,618. Другими словами, длинная сторона в 1,618 раза больше короткой.
Что особенно интересно в золотом прямоугольнике, так это то, что если вы нарисуете внутри него квадрат, как показано выше, оставшаяся часть (синий) будет меньшим золотым прямоугольником.
Продолжим. Мы можем разделить меньший прямоугольник на квадрат и еще меньший золотой прямоугольник:
Мы можем продолжать до тех пор, пока нам нравится делить прямоугольники. А если в каждом квадрате нарисовать четверть круга, то получится спираль. Иллюстрация ниже, вероятно, является одним из самых известных изображений в математике, если не во всей науке. Кривая называется «золотой спиралью».
Золотая спираль представляет собой лоскутное одеяло, состоящее из четвертей круга. (Строго говоря, золотая спираль представляет собой сглаженную версию этой кривой, поэтому никаких педантичных комментариев ниже, пожалуйста!)Вдохновленный классической конструкцией золотой спирали, Харрис, англичанин, начал экспериментировать с процессом разделения прямоугольников. в надежде, что он сможет создать другие эстетически приятные кривые.
Таким образом, вместо того, чтобы начать с прямоугольника, а затем вырезать квадрат, который оставил бы такой же прямоугольник, как мы сделали выше с золотым прямоугольником, он сделал что-то подрывное.
«Вместо того, чтобы вырезать квадрат, я вырезал прямоугольник», — сказал он.
Он сделал следующее: он нашел прямоугольник, который разделился бы на два подобных прямоугольника и квадрат, как показано ниже.
Синий прямоугольник и оранжевый прямоугольник имеют те же пропорции, что и весь прямоугольник, то есть соотношение между сторонами равно 1,325.
Прямоугольник рождает двух одинаковых детей разного размера и квадрат.Так как у нас есть два таких прямоугольника, мы можем продолжить разделение.
При делении мы получаем больше прямоугольников с коэффициентом 1,325.И снова. И опять.
Давайте устроим прямоугольную вечеринку!Еще раз в путь.
Наконец, исходный прямоугольник делится на 34 одинаковых прямоугольника и 33 квадрата.Помните, что для получения золотой спирали мы добавили к квадратам четверть круга? Харрис сделал это и здесь:
Четверть круга идет от угла к соседнему углу каждого квадрата. Глядь, еще одна спираль! Но есть и другие квадраты, которые мы пропустили. Давайте заполним их.
А теперь удалите самую большую дугу, чтобы открыть… фигуру, которую я назову «спираль Харриса».
Спираль Харриса.Харрис был вне себя от радости, когда впервые увидел спираль, потому что она была эстетически привлекательной. Одной из его основных целей было нарисовать разветвляющиеся спирали, которые можно найти в исламском искусстве или работах Густава Климта. Но особенно он был в восторге, потому что пришел к спирали с помощью очень простого математического процесса.
«Нетрудно сделать что-то, чего никто раньше не видел», — сказал он. «Сложнее сделать что-то математически удовлетворительное, чего люди не видели раньше».
Его первым беспокойством было то, что, возможно, спираль нарисовал кто-то другой. «Одна вещь, связанная с математическими открытиями и математическим искусством, заключается в том, что даже если процесс совершенно новый, нет гарантии, что кто-то еще не исследовал его. ”
Выяснилось, что отношение 1,325, которое дает вам прямоугольник, образующий спираль Харриса, было написано — оно известно как «пластическое число», — но Харрис не смог найти предыдущих рисунков спирали. (На самом деле отношение — это число, которое начинается с 1,32472… и продолжается вечно).
Теперь кривая стала его подписью, напечатанной на футболках:
Спиральное племя: Эдмунд Харрис, Джесси Хортон, Элла Ван Хорн и Эзра Ван Хорн (по часовой стрелке от бородатого). Они держат экран для печати футболок.На картах.
Если вы друг Эдмунда, возможно, вы получили одну из этих великолепных открыток.И на номер его машины.
Особое отделение.Еще одним мотивом Харрисса было привнести золотое сечение в более широкое семейство того, что он называет «системами пропорций».
«Золотое сечение — это невероятно хорошо изученный уголок целого города», — сказал он. «Я хотел дать указатели на другие места в этом городе».
Системы пропорций Харриса представляют собой прямоугольники, которые можно разделить только на квадраты и подобные прямоугольники.
В соответствии с этим правилом есть только три возможности для прямоугольников, которые можно разделить на две части.
Первый (разделенный на два одинаковых прямоугольника) представляет собой пропорцию листа бумаги формата А4 (или любого другого числа А) с отношением √2.
Второй (разделенный на квадрат и такой же прямоугольник) — это золотой прямоугольник, а третий (два квадрата) — в форме домино.
Существует 16 вариантов прямоугольников, которые можно разделить на три части.
Вот шесть вариантов, где вы отрезаете большой квадрат и кладете два квадрата/прямоугольника в столбец. Помните, что в любом случае, если есть мини-прямоугольник, он должен иметь те же пропорции, что и весь прямоугольник.
Соотношения прямоугольников и соответствующие уравнения отмечены для каждого прямоугольника.Вот шесть вариантов, где можно отрезать похожий прямоугольник и поместить два квадрата/прямоугольника в столбец.
Внизу слева показана пропорция, которая дает спираль Харриса.А вот четыре варианта, в которых все квадраты/прямоугольники выстраиваются в линию.
Математики узнают отношения, представленные системой пропорций Харриса, как «алгебраические числа» — те числа, которые являются решениями простых уравнений. Харрисс считает, что геометрический подход к алгебраическим числам может привести к их более глубокому пониманию.
«Соотношения уже встречаются в математике и искусстве, что говорит о том, что системы пропорций отражают некоторую идею простоты этих чисел», — сказал Харрис, добавив, что он работает над доказательством того, что каждое алгебраическое число является отношением прямоугольника. принадлежность к системе пропорций.
Я спросил, искал ли Харрис красивые спирали с каким-либо другим соотношением? — Да, но с ограниченным успехом, — вздохнул он. «Проблема в том, чтобы получить набор квадратов, совпадающих в правильном порядке».
Вот что он пока придумал:
Спирали из систем пропорций. Читателям предлагается построить свои собственные спирали, а затем прислать мне футболку.
Чтобы поддерживать связь с этим блогом, подпишитесь на меня в Twitter, нажмите «Нравится» на Facebook или добавьте меня в Google+.
Блог Эдмунда Харриса называется «Демон Максвелла».
Чтобы узнать больше о золотом сечении, вот мой пост о том, что оно было обнаружено в матке, и вот проект, в котором я участвовал, в котором 55 дизайнеров попросили интерпретировать это число. 9Калькулятор золотого прямоугольника Калькулятор золотого прямоугольника рассчитает длину любой стороны и площадь золотого прямоугольника, если вы укажете другую сторону. Прежде чем использовать этот калькулятор, вы должны понять, что такое золотой прямоугольник, как вообще рассчитывать отношения и формулу золотого сечения. Золотой прямоугольник — это прямоугольник, стороны которого находятся в золотом сечении, то есть Калькулятор отношений является эффективным инструментом для помощи в расчете отношений в целом, в то время как калькулятор золотого сечения делает то же самое, что и калькулятор золотого прямоугольника, за исключением нахождения площади прямоугольника. Вот шаги: Интересным аспектом золотого прямоугольника является то, что после удаления квадратной части остается еще один золотой прямоугольник. Кроме того, добавление еще одного квадрата к прямоугольнику со стороной Чтобы построить золотой прямоугольник с помощью циркуля и линейки: Чтобы вычислить ширину золотого треугольника, зная его длину, разделите длину на золотое сечение Около 19 777 см . Что такое золотой прямоугольник?
(a + b)/a = a/b = φ , где a — ширина, a + b — длина прямоугольника, а φ — золотое сечение: φ = (1+√5)/2 . Как использовать наш калькулятор золотого прямоугольника?
a . a + b или сегмент b a × (a + b) a + b — еще один золотой прямоугольник. Калькулятор золотого прямоугольника проверит это. Как нарисовать золотой прямоугольник?
Часто задаваемые вопросы
Как найти ширину золотого прямоугольника?
(1 + √5)/2 , то есть примерно на 1,618 . Какова ширина золотого прямоугольника длиной 32 см?